Rubriky
- Války a válečníci
- Zbraně a zbroj
- Beneš(n)oviny
- Uniformy a modely
- Mrožoviny
- Vojenská technika
- Vojenská symbolika
- Bojové umění
- Miscellanea
- Toluenové opojení - galerie
- Komická sekce
- Hry
- Muzea
Jak letí kulka
Člověk vystřelí, ale kulku řídí Bůh. (Ruské přísloví)
Pokud se zajímáte o zbraně napoleonské doby, pravděpodobně narazíte na citaci tohoto přísloví a při četbě informací o přesnosti tehdejších zbraní (a také nedostatečném střeleckém výcviku tehdejších vojáků) se s ním možná ztotožníte. Nejde ale jen o přesnost tehdejších zbraní, velmi těžko lze dohledat i informace o jejich balistických výkonech. Přestože v této zemi jsou nepochybně tisíce lidí, kteří se zajímají o vojenskou historii a stovky nadšenců v klubech vojenské historie (občas si vystřelí z repliky), najít balistická data zbraní třeba z doby napoleonských válek je prakticky nemožné. Informace v literatuře jsou velmi kusé, lze nalézt pouze zmínky o účinném dostřelu nebo rozptylu při střelbě (např. v [6] nebo [7]), který patrně nejvíce limituje použití tehdejších nepřesných palných zbraní s hladkým vývrtem. Když se hodně snažíte, naleznete údaj o počáteční rychlosti střely. Je to trochu zvláštní, už v druhé polovině osmnáctého století uměli změřit rychlost střely (balistické kyvadlo není nic složitého). Pokud si ale chcete udělat nějakou představu o trajektorii projektilu vystřeleného ze zbraně napoleonské éry, pak nezbývá, než spočítat si ji sám. Samotné výpočty nejsou principiálně ani příliš obtížné. Stačí mít k dispozici počítač s nainstalovaným vhodným tabulkovým procesorem, např. Excelem, základní znalosti fyziky, respektive vnější balistiky, a trošku si pohrát. Už před léty jsem si připravil výpočtový algoritmus, který po zadání počáteční rychlosti, náměru a jednoho koeficientu k, dopočítává celou balistickou křivku, rychlost i složky rychlosti ve vertikální a horizontální ose a navíc úhel trajektorie střely vůči vodorovné ose v daném místě trajektorie. Výpočet se provádí v závislosti na čase postupnými výpočty například po 0,01 s. Výše zmíněný koeficient k je zrychlení střely dělené druhou mocninou rychlosti (předpokládám závislost aerodynamické odporové síly na druhé mocnině rychlosti střely). Koeficient k tedy lze vyjádřit i jednoduchým fyzikálním vztahem k = CxρS/(2m), kde Cx je koeficient aerodynamického odporu střely (obecně ale tento koeficient může záviset na rychlosti), ρ je hustota vzduchu (1,28 kg.m-3 pro normální podmínky), S je plocha příčného průřezu střely a m je hmotnost střely. Tento vztah platí zcela obecně. Pro kulový projektil jej můžeme upravit i do tvaru k = 3Cxρ/(4ρkd), kde ve jmenovateli zlomku ρk je hustota koule a d je její průměr. Tento vztah názorně ukazuje, že balistické vlastnosti kulového projektilu se zlepšují s rostoucí hustotou materiálu a rostoucím průměrem projektilu. Ve svém výpočtovém algoritmu mám zadanou i korekci na změnu hustoty vzduchu s nadmořskou výškou, v níže uvedených výpočtech ale vesměs zůstaneme při zemi.
Mohu tedy provádět následující výpočty. Pokud znám údaje o dané zbrani (úsťovou rychlost, náměr, dostřel, případně jiné relevantní parametry jako propad střely na určité dráze) velmi jednoduše několika postupnými výpočty určím koeficient k pro použitou munici a následně už mohu provádět libovolné výpočty pro danou zbraň. Ověřoval jsem si správnou funkci výpočtového algoritmu pomocí dat z literatury, např. [1] nebo [2]. Vždy jsem použil nějaká data jako vstupní a dopočtená data jsem srovnával s tabelovanými. Ověřil jsem si tedy funkci algoritmu pro širokou škálu zbraní od ráže 5,56 mm po 406 mm, shoda výsledků je velmi dobrá. Samozřejmě, nutnou podmínkou pro to aby výpočty fungovaly je konstantnost koeficientu odporu vzduchu Cx po dobu letu střely (tedy jeho nezávislost na rychlosti letu). Tato podmínka byla pro uvedené výpočty zřejmě alespoň přibližně splněna, protože rychlost letu střel zůstávala nadzvuková.
Druhý možný postup spočívá ve výpočtu koeficientu k podle výše uvedeného vztahu, pokud znám příslušné parametry pro danou střelu (v našem případě tedy pro kouli). Pak je, při znalosti úsťové rychlosti a náměru, možno dopočítat balistickou křivku i jiné parametry trajektorie střely. Zásadní problém, který v tomto případě nastane, je skutečnost, že koeficient odporu vzduchu pohybující se střely se významně mění především v transsonické oblasti (při přechodu od rychlostí menších než rychlost zvuku k větším nebo naopak). V supersonické oblasti rychlostí je součinitel odporu zpravidla dvojnásobný než pro rychlosti menší než rychlost zvuku.
Přestože jsem měl k dispozici několik knih o vnější balistice, pro řešení daného problému se ukázala jako nejpřínosnější publikace [3], v níž jsem nalezl malý graf závislosti koeficientu aerodynamického odporu koule na rychlosti. Tuto grafickou závislost jsem pro rychlosti do 300 m.s-1aproximoval lineární závislostí Cx = 0,37 + 0,00212.v, kde v je okamžitá rychlost střely. Pro vyšší rychlosti vyhovuje konstantní Cx = 1,02. Chyba těchto aproximací by neměla přesáhnout 5 % a uvedenou aproximaci jsem zavedl do svého výpočtového algoritmu.
Pro porovnání jsem zvolil dvě zbraně. Dvanáctiliberní kanon Gribeauval, který má ráži 121,3 mm, průměr koule 118,1 mm, hmotnost koule 5,87 kg (údaje z [4], str.12) a počáteční rychlost střely 415 m.s-1 (podle [5] str. 31).
Druhou zbraní je mušketa Charville AN IX. Zbraň má ráži 17,5 mm, střílí olověnou kouli průměru 16,5 mm o hmotnosti 27,17 g, prachová náplň je 12,24 g (viz [8]). Jediný údaj o počáteční rychlosti střely vystřelené z této muškety se mi podařilo dohledat na internetu, zmiňuje se o maximální rychlosti 1400 stop za sekundu, tedy 427 m.s-1. Mušketa má výrazně delší hlaveň než kanon (65 ráží, kanon má 17 ráží) i relativně těžší prachovou náplň (prachová náplň muškety má 45 % hmotnosti náboje, u kanonů se zpravidla udává, že náplň měla třetinu hmotnosti náboje). To jsou okolnosti, které by svědčily o větší počáteční rychlosti střely z muškety než z kanonu. Na druhé straně, výstřel z muškety trvá kratší dobu, neboť hlaveň má menší délku. To může způsobit, že prach nestačí vyhořet tak dobře, jako v případě výstřelu z kanonu. Výpočty, které čtenáři nabízím, jsou ovšem především srovnávací a ilustrativní a zvolil jsem proto pro obě zbraně stejnou počáteční rychlost střely, 420 m.s-1. Při posuzování předložených závěrů je nutno mít určitou nejistotu vstupních parametrů (objektivně způsobenou nedostatkem relevantních údajů) na zřeteli.
Při výpočtech jsem předpokládal, že ústí zbraní je ve výšce 1 m nad terénem a výsledky výpočtů pro jednotlivé analyzované situace jsou znázorněny v následujících grafech.
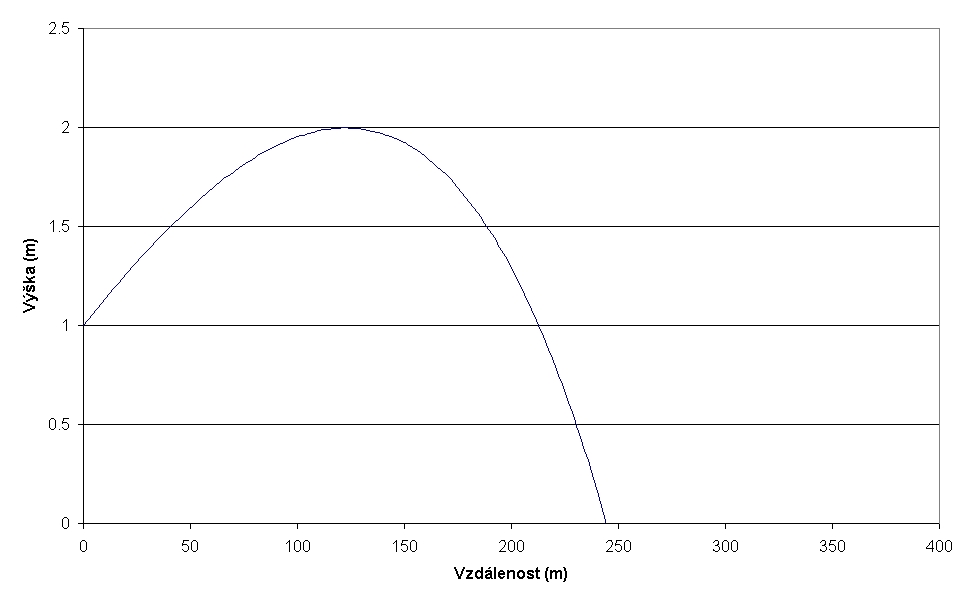
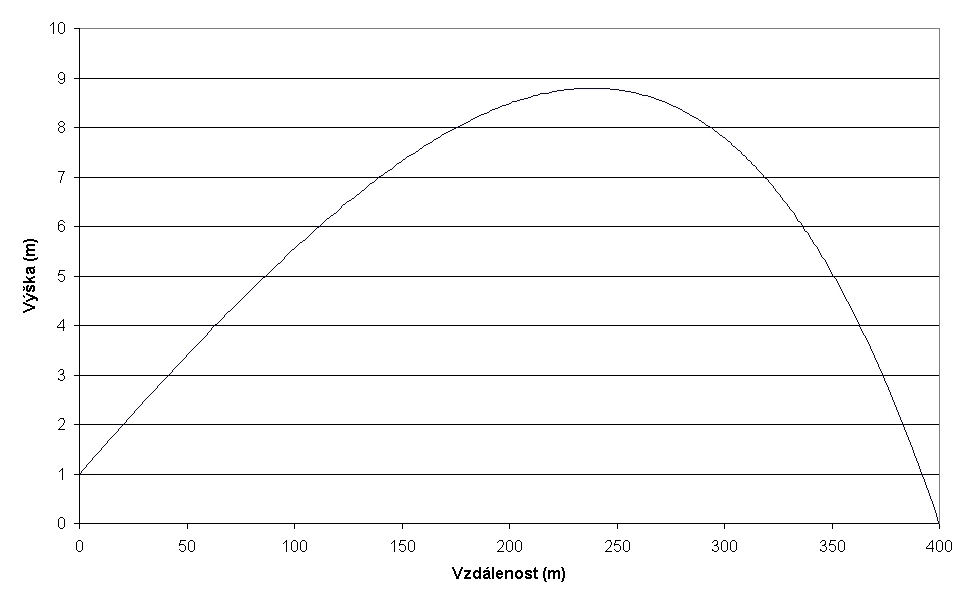
Graf č. 1: Trajektorie střely z muškety při střelbě s metnou výškou 2 m.
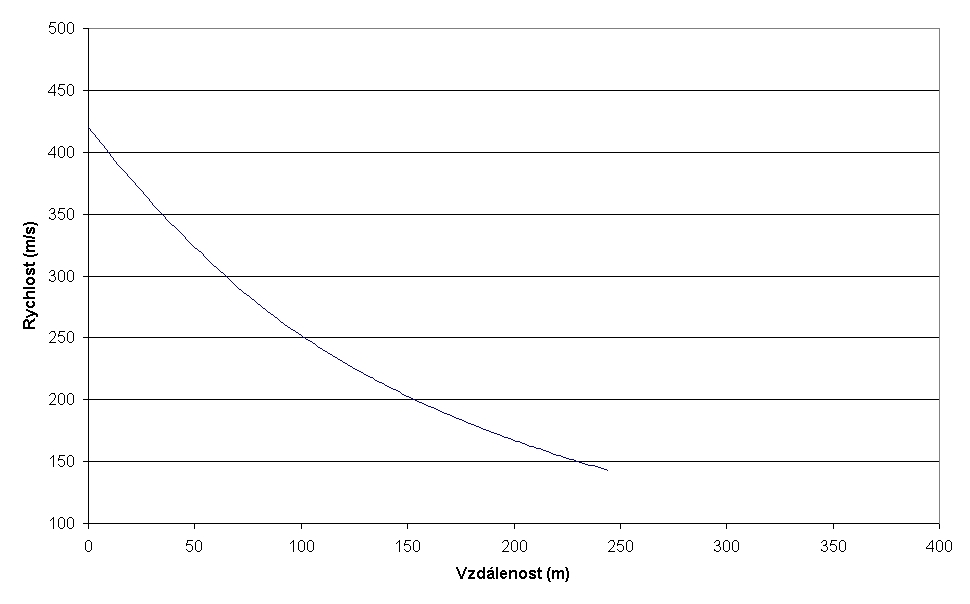
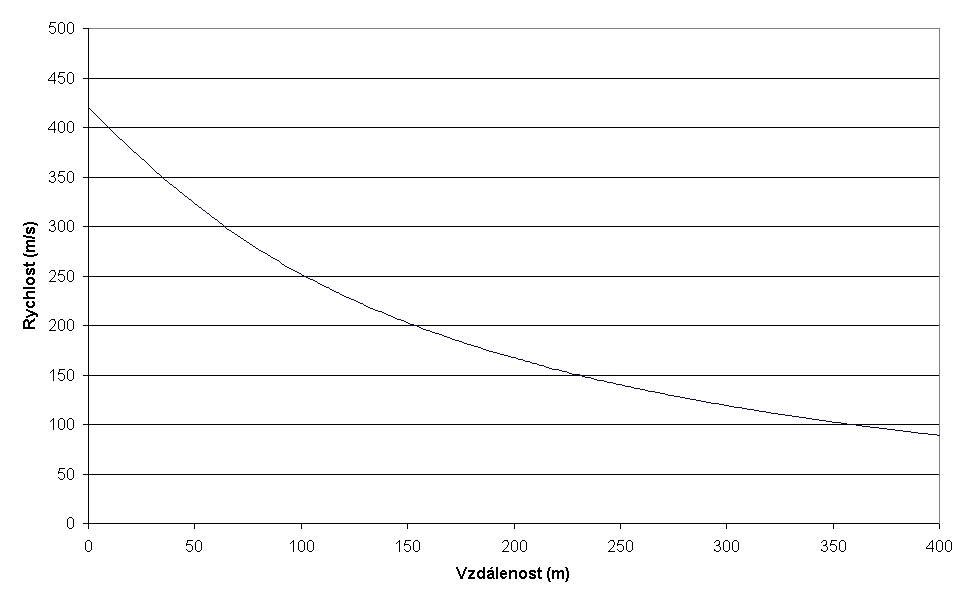
Graf č. 2: Rychlost střely z muškety v závislosti na vzdálenosti, střelba s metnou výškou 2 m.
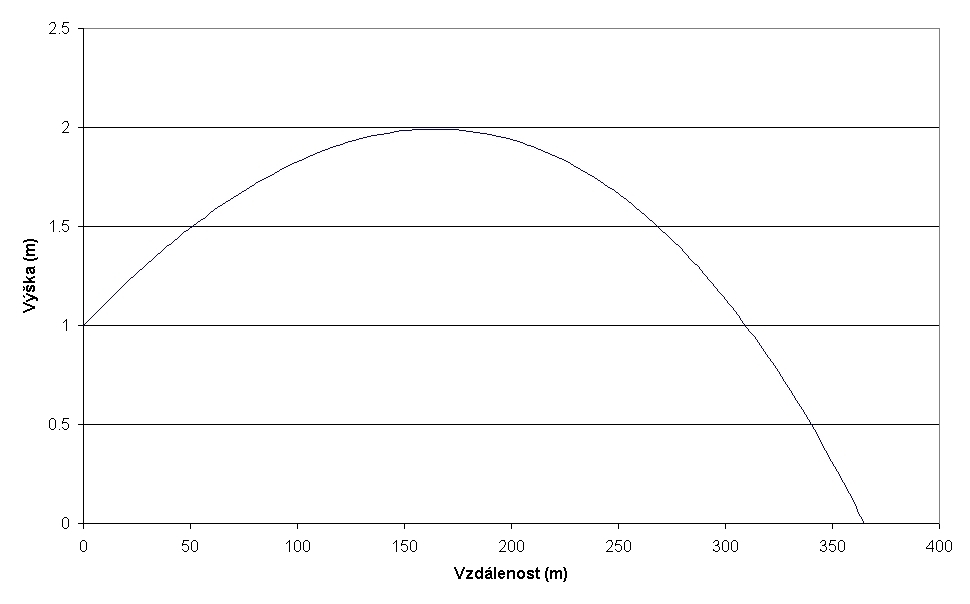
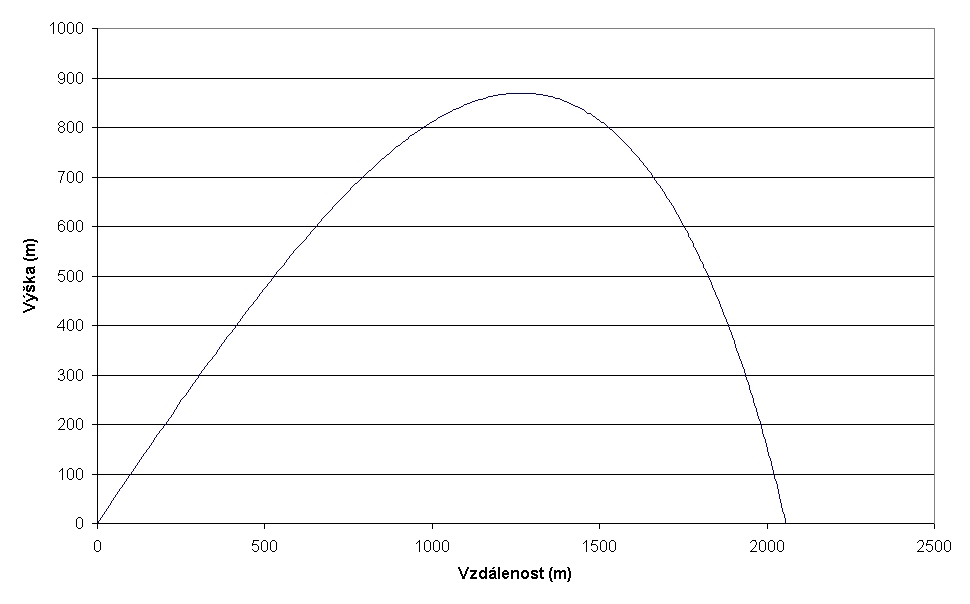
Graf č. 3: Trajektorie střely z kanonu při střelbě s metnou výškou 2 m.
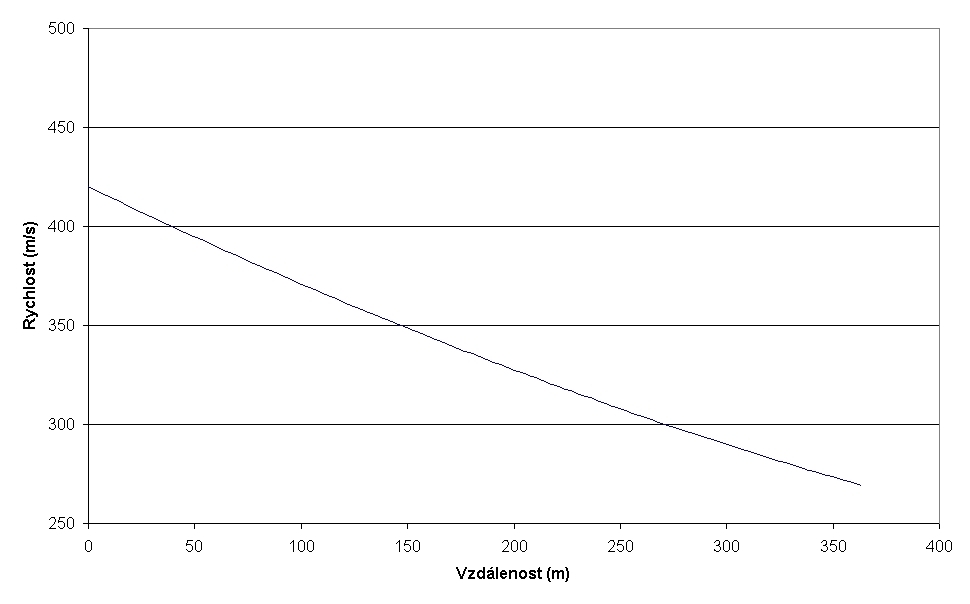
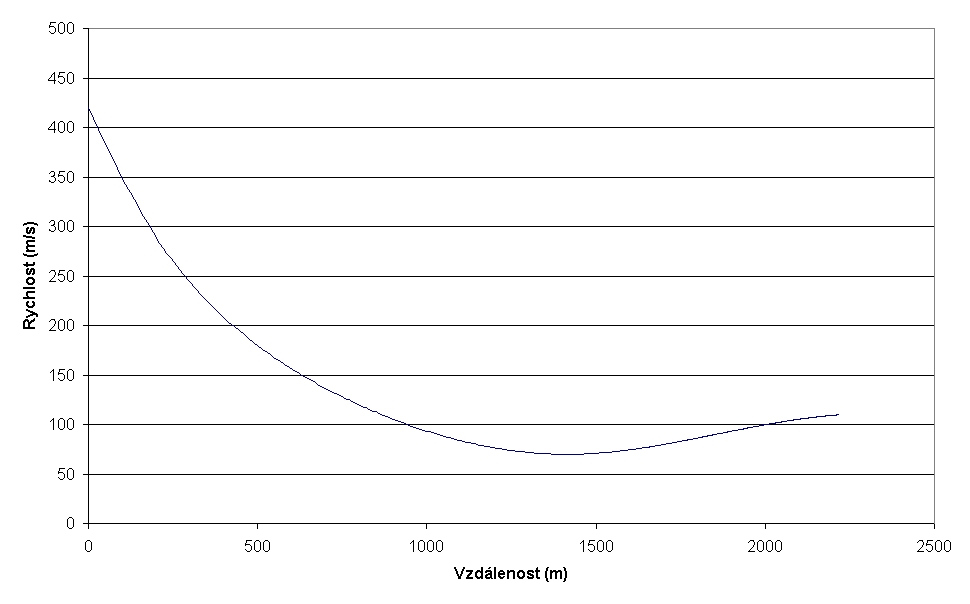
Graf č. 4: Rychlost střely z kanonu v závislosti na vzdálenosti, střelba s metnou výškou 2 m.
První analyzovaný problém byla střelba z muškety a kanonu s předepsanou metnou výškou 2 m, při ústí hlavně 1 m nad terénem. Výsledky jasně ukazují, že kanon dostřelí na větší vzdálenost a jeho projektil ztratí daleko méně energie. To jsou závěry celkem očekávatelné. V literatuře se občas objevují zmínky o střelbě dvojitým nábojem (kulí a kartáčem zároveň). V této situaci by kule měla předběhnout kartáčové kuličky (počáteční rychlost takového dvojitého projektilu bude ale pochopitelně nižší). Kanon dosahuje za daných podmínek dostřelu asi 370 m při náměru 0,640 dopadový úhel je 1,240, to jsou parametry určitě vhodné pro ricochetovou střelbu.
Druhý analyzovaný problém byla střelba na vzdálenost maximálního účinného dostřelu, zvolil jsem v souladu s údaji vyskytujícími se v literatuře 400 m pro mušketu a 1000 m pro kanón.
Graf č. 5: Trajektorie střely z muškety při střelbě na vzdálenost maximálního účinného dostřelu
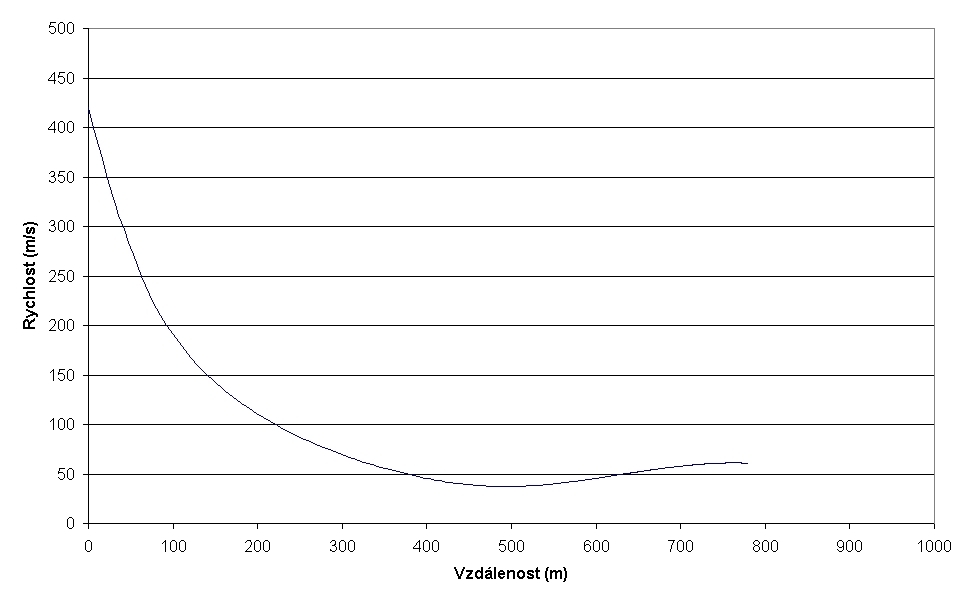
Graf č. 6: Rychlost střely z muškety v závislosti na vzdálenosti, střelba na vzdálenost max. účinného dostřelu.
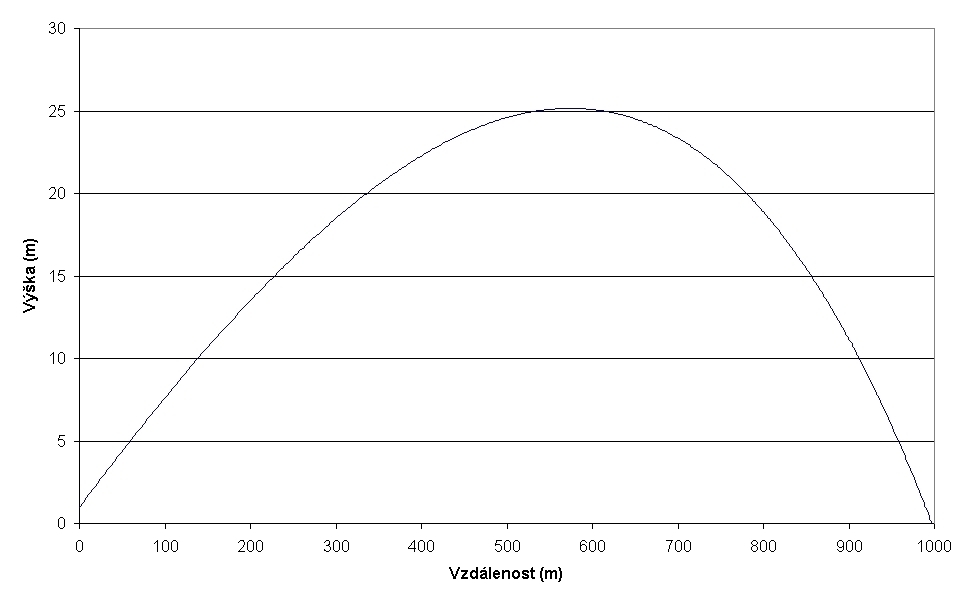
Graf č. 7: Trajektorie střely z kanonu při střelbě na vzdálenost max. účinného dostřelu.
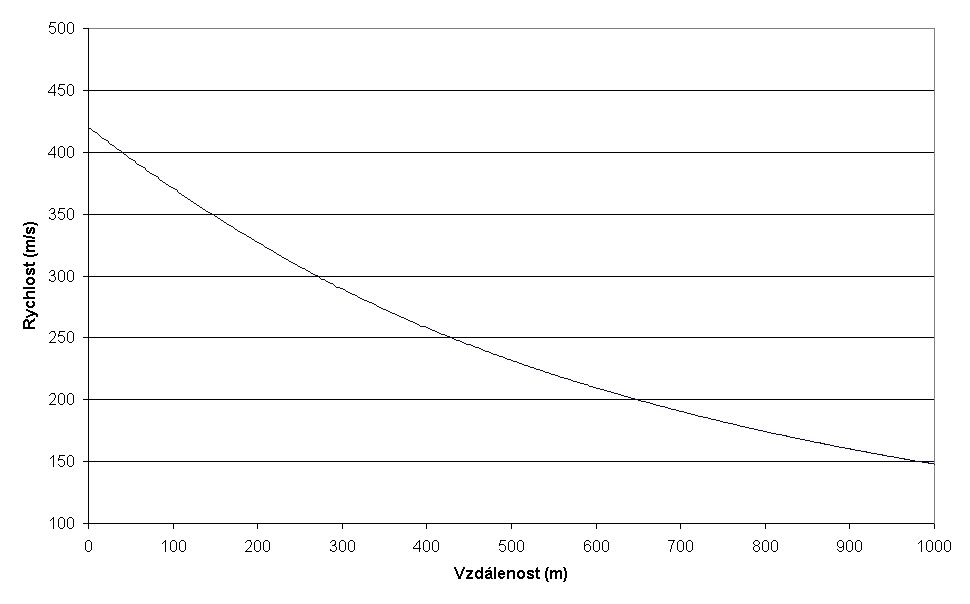
Graf č. 8: Rychlost střely z kanonu v závislosti na vzdálenosti, střelba na vzdálenost max. účinného dostřelu.
Z grafů č. 5. a 7. vidíme, že při střelbě na tyto vzdálenosti už musíme mířit hodně vysoko nad cíl, náměr je 2,830 u pušky a 3,950 u kanonu. U kanonu můžeme ještě pravděpodobně očekávat možnost střelby na odraz (ricochetová střelba).
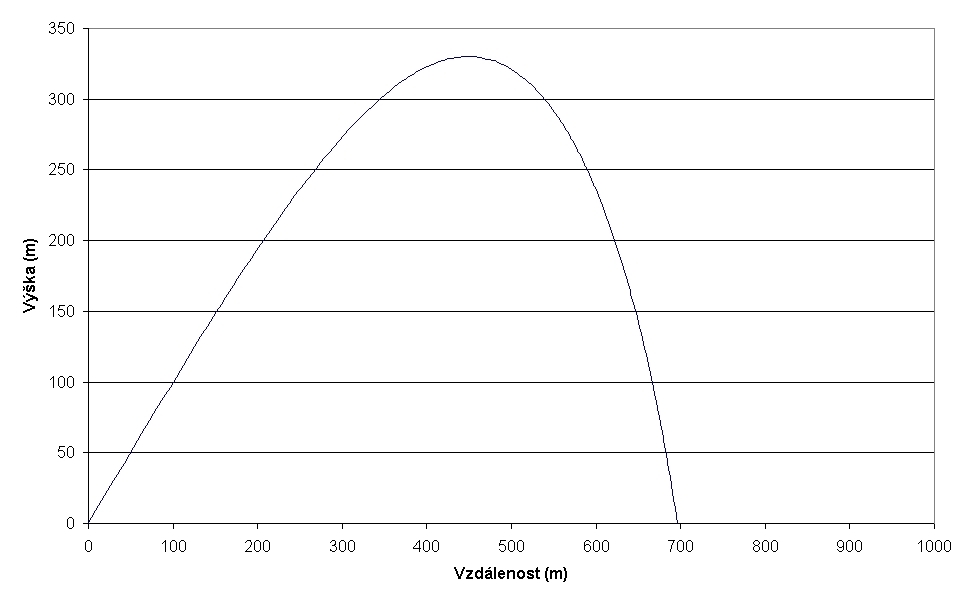
Graf č. 9: Trajektorie střely z muškety při střelbě s náměrem 450.
Graf č. 10: Rychlost střely z muškety v závislosti na vzdálenosti, střelba s náměrem 450.
Graf č. 11: Trajektorie střely z kanonu při střelbě s náměrem 450.
Graf č. 12: Rychlost střely z kanonu v závislosti na vzdálenosti, střelba s náměrem 450.
Posledním analyzovaným problémem je střelba s elevací 450. Ve vakuu by střela s uvažovanou rychlostí (420 m.s-1) měla dostřel 17840 m. Připomeňme, že v odporujícím prostředí není elevace 450 elevací odpovídající největšímu dostřelu, toho se dosahuje při trošku menších úhlech (v našem případě asi 410), rozdíly jsou však velmi malé. Původně mně k tomuto výpočtu přiměly zmínky v literatuře [6] (str. 46) a [8], podle kterých při střelbě z muškety na vzdálenost 800 – 900 kroků (předpisový krok činí 66 cm) musel střelec mířit asi metr nad cíl. Připadalo mi to divné, protože i moderní náboje mají při střelbě na tyto vzdálenosti větší propady. Začal jsem při výpočtech zvětšovat náměr a zjistil jsem, že tato vzdálenost se blíží maximálnímu dostřelu muškety. Při pohledu na graf č. 9 je zřejmé, že citované tvrzení je mylné. Povšimněme si ještě dopadových rychlostí střel. U muškety i u kanonu se prakticky rovnají ustálené rychlosti pádu daného projektilu ve vzduchu. V případě kulky z muškety je to zhruba 60 m.s-1, což je pro srovnání trochu větší rychlost než je ustálená rychlost pádu lidského těla ve vzduchu (ta činí zhruba 50 m.s-1). V případě dělové koule je ustálená rychlost pádu ve vzduchu asi 120 m.s-1. Kanon má podle [5] (str. 31) maximální dostřel 3000 m (není udán náměr), přestože lafeta podle mého názoru není konstruována pro střelbu s náměrem kolem 400 a mé výpočty svědčí o menším maximálním dostřelu.
Myslím, že jsem spočítal maximum, které bylo s danými vstupními daty možné. Teď už je na mušketýrech (a dělostřelcích) aby nabíjeli, stříleli a porovnávali.
Literatura:
[1] Kuchyňka, A.: Střelivo zvláštního určení, Vydavatelství Radka Kuchyňková, Hustopeče 2001
[2] www.nawveaps.com
[3] Komenda J., Vítek R., Rydlo M.: Vnější balistika loveckých, sportovních a obranných zbraní, Ostrava 2006
[4] Chartrand, R.: Napoleonova děla 1792-1815, Grada Publishing, Praha 2008
[5] Karlický, V.: Salvy duní, Naše vojsko, Praha 1979
[6] Kovařík, J.: 1812 Napoleonovo ruské tažení, Hart, Praha 2001
[7] Kovařík, J.:Napoleonova tažení I, Akcent, Třebíč 2003
[8] http://napoleonika.cz/content/view/43/10/lang,cz/
Foto týdne

Výročí: 18. 4. 1945 Do prostoru Ašského výběžku vstoupili první američtí vojáci – průzkumná hlídka 3. praporu 358. pluku 90. divize americké armády pod vedením generála Pattona.
Recenze týdne
Vydalo nakladatelství Academia 2023.